

Задача про мышей — математическая головоломка, по условию которой несколько мышей (или комаров, собак, ракет), расположены в углах правильного многоугольника. Каждая мышь начинает двигаться в направлении ближайшего соседа (по часовой стрелке или против часовой стрелки). В задаче требуется определить момент времени, когда мыши встретятся.
Наиболее распространённый вариант задачи — когда мыши начинают двигаться из углов единичного квадрата, причём скорость мышей одинакова. В этом случае все они встречаются в один и тот же момент времени, поскольку расстояние между двумя соседними мышами всегда уменьшается, а скорость постоянна. В общем, для правильного многоугольника с n сторонами, расстояние между соседними мышами уменьшается со скоростью 1 − cos(2π/n), и таким образом, они встретятся через время 1/(1 − cos(2π/n))[1][2].
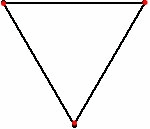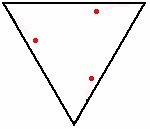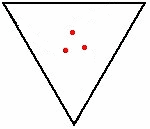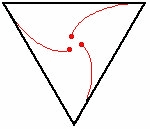
Траектория мышей
Для всех правильных многоугольников мыши двигаются по логарифмической спирали, которая сходится в центре многоугольника[3]. При увеличении количества мышей, и если мыши движутся в направлении не своих ближайших соседей, определить их траектории сложнее.


См. также
Примечания
- ↑ Гамов, Георгий Антонович, Штерн, Марвин (1958), Математическая головоломка, Нью-Йорк: Viking press, с. 112—114
- ↑ Эдвард Лукас, (1877), «Задача про трёх собак», Nouv. Corresp. Math. 3: с. 175—176
- ↑ Задача про мышей. MathWorld.
Ссылки
- Мания преследования[неавторитетный источник?] — расширенная задача про мышей.
| Это заготовка статьи по геометрии. Вы можете помочь проекту, дополнив её. |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .