WikiSort.ru - Не сортированное

Точечная группа в трёхмерном пространстве

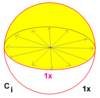
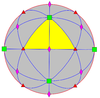
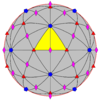
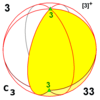
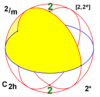
Симметрии-инволюции Cs, (*) [ ] =	Циклическая симметрия Cnv, (*nn) [n] =	Диэдральная симметрия Dnh, (*n22) [n,2] =
Группы многогранников, [n,3], (*n32)
Тетраэдральная симметрия Td, (*332) [3,3] =	Октаэдральная симметрия Oh, (*432) [4,3] =	Икосаэдральная симметрия Ih, (*532) [5,3] =

Группы сферической симметрии также называются точечными группами в трёхмерном пространстве^[en]*, однако эта статья рассматривает только конечные симметрии. Существует пять фундаментальных классов симметрии, которыми обладают треугольные фундаментальные области: диэдрическая, циклическая, тетраэдральная симметрия, октаэдральная симметрия^[en] и икосаэдральная симметрия^[en].

Статья перечисляет группы согласно символам Шёнфлиса, записи Коксетера^{[en] [1]}, орбифолдной записи^{[en] [2]} и порядка. Конвей использовал вариант записи Шёнфлиса, основанном на алгебраической структуре группы кватернионов, с обозначениями одной или двумя заглавными буквами и полным набором нижних числовых индексов. Порядок группы обозначается индексом, если только он не удваивается символом плюс-минус ("±"), который подразумевает центральную симметрию ^[3].

Символика Германа — Могена (интернациональная запись) приводится также. Группы кристаллографии, 32 в общем числе, являются подмножеством с элементами порядка 2, 3, 4 и 6 ^[4].

Симметрии-инволюции

Имеется четыре симметрии, которые являются обратными себе, т.е. инволюциями: тождественное преобразование (C₁), зеркальная симметрия (C_s), вращательная симметрия (C₂), и центральная симметрия (C_i).

Инт. Геом. [5] Орб. Шёнф. Конвей Кокс. Пор. Фунд. область 1 1 11 C1 C1 ][ [ ]+ 1 2 2 22 D1 = C2 D2 = C2 [2]+ 2

Инт. Геом. Ориб. Шёнф. Конвей Кокс. Пор. Фунд. область 1 22 × Ci = S2 CC2 [2+,2+] 2 2 = m 1 * Cs = C1v = C1h ±C1 = CD2 [ ] 2

Циклическая симметрия

Существуют четыре бесконечных семейства циклической симметрии^[en] с n=2 и выше. (n может быть равен 1 как особый случай нет симметрии)

Инт. Гео Орб. Шёнф. Конвей. Кокс. Пор. Фунд. область 2 2 22 C2 = D1 C2 = D2 [2]+ [2,1]+ 2 mm2 2 *22 C2v = D1h CD4 = DD4 [2] [2,1] 4 4 42 2× S4 CC4 [2+,4+] 4 2/m 22 2* C2h = D1d ±C2 = ±D2 [2,2+] [2+,2] 4

Инт. Геом. Орб. Шёнф. Конвей Кокс. Пор. Фунд. область 3 4 5 6 n 3 4 5 6 n 33 44 55 66 nn C3 C4 C5 C6 Cn C3 C4 C5 C6 Cn [3]+ [4]+ [5]+ [6]+ [n]+ 3 4 5 6 n 3m 4mm 5m 6mm - 3 4 5 6 n *33 *44 *55 *66 *nn C3v C4v C5v C6v Cnv CD6 CD8 CD10 CD12 CD2n [3] [4] [5] [6] [n] 6 8 10 12 2n 3 8 5 12 - 62 82 10.2 12.2 2n.2 3× 4× 5× 6× n× S6 S8 S10 S12 S2n ±C3 CC8 ±C5 CC12 CC2n / ±Cn [2+,6+] [2+,8+] [2+,10+] [2+,12+] [2+,2n+] 6 8 10 12 2n 3/m=6 4/m 5/m=10 6/m n/m 32 42 52 62 n2 3* 4* 5* 6* n* C3h C4h C5h C6h Cnh CC6 ±C4 CC10 ±C6 ±Cn / CC2n [2,3+] [2,4+] [2,5+] [2,6+] [2,n+] 6 8 10 12 2n

Диэдральная симметрия

Существует три бесконечных семейства с диэдральной симетрией^[en] с n равным 2 и выше. (n может быть равен 1 как специальный случай)

Инт. Геом. Орб. Шёнф. Конвей Кокс. Пор. Фунд. область 222 2.2 222 D2 D4 [2,2]+ 4 42m 42 2*2 D2d DD8 [2+,4] 8 mmm 22 *222 D2h ±D4 [2,2] 8

Инт. Геом. Орб. Шёнф. Конвей Кокс. Пор. Фунд. область 32 422 52 622 3.2 4.2 5.2 6.2 n.2 223 224 225 226 22n D3 D4 D5 D6 Dn D6 D8 D10 D12 D2n [2,3]+ [2,4]+ [2,5]+ [2,6]+ [2,n]+ 6 8 10 12 2n 3m 82m 5m 12.2m 62 82 10.2 12.2 n2 2*3 2*4 2*5 2*6 2*n D3d D4d D5d D6d Dnd ±D6 DD16 ±D10 DD24 DD4n / ±D2n [2+,6] [2+,8] [2+,10] [2+,12] [2+,2n] 12 16 20 24 4n 6m2 4/mmm 10m2 6/mmm 32 42 52 62 n2 *223 *224 *225 *226 *22n D3h D4h D5h D6h Dnh DD12 ±D8 DD20 ±D12 ±D2n / DD4n [2,3] [2,4] [2,5] [2,6] [2,n] 12 16 20 24 4n

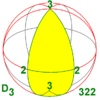
Симметрии многогранников

Существует три типа симметрии многогранников^[en]: тетраэдральная симметрия, октаэдральная симметрия^[en] и икосаэдральная симметрия^[en], названные по правильным многогранникам с треугольными гранями, которые обладают такими симметриями.

Тетраэдральная симметрия Инт. Геом. Орб. Шёнф. Конвей Кокс. Пор. Фунд. область 23 3.3 332 T T [3,3]+ = [4,3+]+ 12 m3 43 3*2 Th ±T [4,3+] 24 43m 33 *332 Td TO [3,3] = [1+,4,3] 24

Октаэдральная симметрия[en] Инт. Геом. Орб. Шёнф. Конвей Кокс. Пор. Фунд. область 432 4.3 432 O O [4,3]+ = [[3,3]]+ 24 m3m 43 *432 Oh ±O [4,3] = [[3,3]] 48 Икосаэдральная симметрия[en] Инт. Геом. Орб. Шёнф. Конвей Кокс. Пор. Фунд. область 532 5.3 532 I I [5,3]+ 60 532/m 53 *532 Ih ±I [5,3] 120

См. также

• Кристаллографическая точечная группа симметрии
• Группа треугольника
• Список планарных групп симметрии^[en]
• Точечные группы в двухмерном пространстве^[en]

Примечания

Литература

• Peter R. Cromwell, Polyhedra (1997), Appendix I
• Donald E. Sands. Crystal Systems and Geometry // Introduction to Crystallography. — Mineola, New York: Dover Publications, Inc., 1993. — С. 165. — ISBN 0-486-67839-3.

• Джон Х. Конвей, Дерек А. Смит. О кватернионах и октавах = On Quaternions and Octonions. — Москва: МЦНМО, 2009. — ISBN 978-5-94057-517-7.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. The Symmetries of Things. — New-York: A K Peters/CRC Press,, 2008. — ISBN 978-1-56881-220-5.
• H.S.M. Coxeter. Kaleidoscopes: Selected Writings of H.S.M. Coxeter / F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss,. — Wiley-Interscience Publication,, 1995. — ISBN 978-0-471-01003-6.
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
• Norman Johnson. Chapter 11: Finite symmetry groups // Geometries and Transformations. — 2015.
• D. Hestenes^[en], J. Holt. The Crystallographic Space groups in Geometric algebra // Journal of Mathematical Physics. — 2007. — Вып. 48, 023514.

Внешние ссылки

• Finite spherical symmetry groups
• Weisstein, Eric W. Schoenflies symbol (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Crystallographic point groups (англ.) на сайте Wolfram MathWorld.
• Simplest Canonical Polyhedra of Each Symmetry Type, by David I. McCooey

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.