Гипотеза Ловаса о гамильтоновом цикле — классическая гипотеза в теории графов.
Сформулирована в четвёртом томе «Искусства программирования», но, скорее всего, была известна гораздо раньше.
Формулировка
Каждый конечный связный вершинно-транзитивный граф содержит гамильтонов путь.
Вариации и обобщения
- Любой конечный связный вершинно-транзитивный граф, кроме пяти исключений, содержит гамильтонов цикл; исключения составляют:
- Полный граф ,
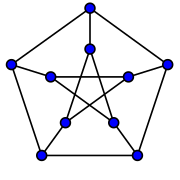
- Граф Петерсена и граф, полученный из него заменой каждой вершины на треугольник,
- Граф Коксетера и граф, полученный из него заменой каждой вершины на треугольник.
|
Ни одно из пяти исключений не является графом Кэли. Это наблюдение приводит к более слабой версии гипотезы
- Любой граф Кэли конечной группы содержит гамильтонов цикл.
Для ориентированных графов Кэли гипотеза не верна.
Частные случаи
- Известно, что ориентированный граф Кели абелевой группы имеет гамильтонов путь.
- С другой стороны, циклические группы, порядок которых не является степенью простого числа, допускают ориентированный граф Кэли без гамильтонова цикла.[1]
- В 1986 году Д. Витте доказал, что гипотеза верна для графов Кэли p-групп.
- Вопрос остаётся открытым для диэдральных групп.
Известно, что для симметрической группы гипотеза верна для следующих наборов образующих:
- (длинный цикл и транспозиция).
- (образующие Кокстера). В этом случае гамильтонов цикл строится алгоритмом Штайнхаусa — Джонсона — Троттера[en].
- .
Ссылки
- ↑ Holsztyński, W. & Strube, R. F. E. (1978), "Paths and circuits in finite groups", Discrete Mathematics Т. 22 (3): 263–272, DOI 10.1016/0012-365X(78)90059-6.
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .