
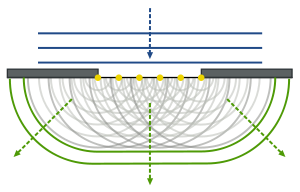
Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.
Описание
Принцип Гюйгенса является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка фронта (поверхности, достигнутой волной) является вторичным (то есть новым) источником сферических волн. Огибающая фронтов волн всех вторичных источников становится фронтом волны в следующий момент времени.
Принцип Гюйгенса в таком виде объясняет распространение волн, согласующееся с законами геометрической оптики, но не может достаточно полно, а тем более количественно, объяснить явлений дифракции. Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.
Принцип Гюйгенса — Френеля формулируется следующим образом:
|
Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн. |
Густав Кирхгоф придал принципу Гюйгенса строгий математический вид, показав, что его можно считать приближенной формой теоремы, называемой интегральной теоремой Кирхгофа.
Фронтом волны точечного источника в однородном изотропном пространстве является сфера. Амплитуда возмущения во всех точках сферического фронта волны, распространяющейся от точечного источника, одинакова.
Дальнейшим обобщением и развитием принципа Гюйгенса является формулировка через интегралы по траекториям, служащая основой современной квантовой механики.
См. также
Примечания
Ссылки
- Гюйгенса - Френеля принцип // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- Гюйгенса - Френеля принцип — статья из Физической энциклопедии.
- Видео, наглядно описывающее принцип Гюйгенса - Френеля // Центральная кинолаборатория школьного фильма РСФСР, Министерство просвещения, Москва.
| Это заготовка статьи по оптике. Вы можете помочь проекту, дополнив её. |
В этой статье не хватает ссылок на источники информации. |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .