
Теорема о шести окружностях — теорема в геометрии треугольника.
Формулировка
Рассмотрим цепь из окружностей, каждая из которых касается двух сторон данного треугольника, а также предыдущей окружности в цепи. Тогда эта цепь замыкается, в том смысле, что шестая окружность касается первой[1].
Вариации и обобщения
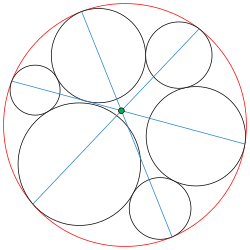
- Теорема о семи окружностях
Проведя цепочку из шести черных окружностей (см. рис. справа), каждая из которых касается седьмой окружности (красная), и каждая из которых касается двух соседних окружностей, три линии (синие), проведенные между противоположными парами точек касания с седьмой окружностью, пересекаются в одной точке (зеленая). Хотя элементарная по сути эта теорема не была известна вплоть до 1974 года [2],[3].
Если радиусы трёх окружностей приблизятся к бесконечности, три окружности превратятся в прямые линии — в стороны треугольника, а центральная окружность — во вписанную окружность этого треугольника. Тогда три линии, соединяющие противоположные точки касания (точки касания со сторонами образованного треугольника с соответствующими противоположными им вершинами треугольника), также пересекутся в одной точке (как чевианы треугольника). Это соответствует последнему рисунку справа внизу, где, кстати, видны и три указанные чевианы, пересекающиеся в одной точке.
См. также
Примечания
- ↑ Evelyn CJA, Money-Coutts GB, Tyrrell JA. The Seven Circles Theorem and Other New Theorems. — London : Stacey International, 1974. — P. 49-58. — ISBN 978-0-9503304-0-2.
- ↑ Evelyn, C. J. A.; Money-Coutts, G. B.; and Tyrrell, J. A. "The Seven Circles Theorem." §3.1 in The Seven Circles Theorem and Other New Theorems. London: Stacey International, pp. 31-37, 1974.
- ↑ Seven circles theorem. Теорема о шести окружностях (англ. яз.)// https://en.wikipedia.org/wiki/Seven_circles_theorem
Литература
- Wells D. The Penguin Dictionary of Curious and Interesting Geometry. — New York : Penguin Books, 1991. — P. 231. — ISBN 0-14-011813-6.
Ссылки
- Weisstein, Eric W. Six Circles Theorem (англ.) на сайте Wolfram MathWorld.
- The Six Circle Theorem revisited by D. Ivanov and S. Tabachnikov
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .