WikiSort.ru - Не сортированное

В теории категорий коядро — это понятие, двойственное к ядру — ядро является подобъектом прообраза, а коядро — факторобъектом образа. Интуитивно, при поиске решения уравнения ${\displaystyle f(x)=y}$ коядро определяет число ограничений, которым должен удовлетворять y, чтобы данное уравнение имело решение.

Определение

Пусть C — категория с нулевыми морфизмами. Тогда коядро морфизма f : X → Y — это коуравнитель его и нулевого морфизма 0 : X → Y. Более явно, выполняется следующее универсальное свойство:

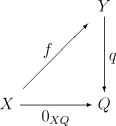
Коядро f : X → Y — это морфизм q : Y → Q, такой что:

• q o f — нулевой морфизм из X в Q;

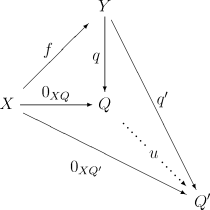
• Для любого морфизма ${\displaystyle q':Y\to Q'}$ , такого что ${\displaystyle q'\circ f}$  — нулевой существует единственный морфизм ${\displaystyle u:Q\to Q'}$ , такой что следующая диаграмма коммутативна:

Как и другие универсальные конструкции, коядро существует не всегда, но если существует, то определено с точностью до изоморфизма.

Как и любые коуравнители, коядро — всегда эпиморфизм. Обратно, эпиморфизм называется нормальным (иногда — конормальным), если он является коядром некоторого морфизма. Категория называется конормальной, если любой эпиморфизм в ней нормален.

Специальные случаи

В абелевой категории образ и кообраз морфизма задаются как

${\displaystyle \mathrm {im} (f)=\ker(\mathrm {coker} f)}$

${\displaystyle \mathrm {coim} (f)=\mathrm {coker} (\ker f)}$ .

В частности, любой эпиморфизм является своим собственным коядром.

Литература

• С. Маклейн Категории для работающего математика, — М.: ФИЗМАТЛИТ, 2004. — 352 с. — ISBN 5-9221-0400-4.
• Paolo Aluffi Algebra: Chapter 0 (Graduate Studies in Mathematics). — 2009, ISBN 0-8218-4781-3.