WikiSort.ru - Не сортированное

В теории графов рёберное покрытие графа — это множество рёбер, в котором каждая вершина графа инцидентна по меньшей мере одному ребру покрытия. В информатике задача о минимальном рёберном покрытии — это задача поиска рёберного покрытия минимального размера. Задача является задачей оптимизации, принадлежит классу задач покрытия^[en] и может быть решена за полиномиальное время.

Определение

Формально, рёберное покрытие графа G — это множество рёбер C, такое, что каждая вершина графа G инцидентна по меньшей мере одному ребру из C. Множество C называется покрытием вершин графа G. Следующий рисунок показывает рёберное покрытие двух графов.

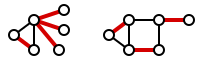
Минимальное рёберное покрытие — это рёберное покрытие наименьшего размера. Число рёбер в минимальном рёберном покрытии графа называется числом рёберного покрытия и обозначается через ${\displaystyle \rho (G)}$ (в книге Свами, Тхулалирамана — ${\displaystyle \beta _{1}(G)}$ ). Следующий рисунок показывает примеры минимальных рёберных покрытий.

Заметим, что покрытие правого графа является не только рёберным покрытием, но и паросочетанием. Более того, это паросочетание является совершенным паросочетанием — в нём каждая вершина инцидентна в точности одному ребру паросочетания. Совершенное паросочетание (если существует) всегда является минимальным рёберным покрытием.

Свойства

• В связном двудольном графе общее число рёбер в минимальном рёберном покрытии и максимальном паросочетании равно числу вершин графа.

Алгоритмы

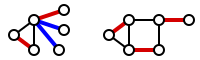
Наименьшее рёберное покрытие можно найти за полиномиальное время путём нахождения максимального паросочетания с последующим добавлением рёбер с помощью жадного алгоритма для покрытия оставшихся вершин ^[1][2]. На следующем рисунке максимальное паросочетание показано красным цветом. Дополнительные рёбра, которые добавлены для покрытия непокрытых вершин, показаны синим цветом (в графе справа максимальное паросочетание является совершенным паросочетанием, в котором все вершины уже покрыты, так что нет необходимости в дополнительных рёбрах.)

С другой стороны, близкая задача нахождения минимального вершинного покрытия является NP-трудной задачей ^[1]

См. также

• Задача о вершинном покрытии
• Задача о покрытии множества — задача о рёберном покрытии является частным случаем задачи о покрытии множества – элементами генеральной совокупности являются вершины, а каждое подмножество покрывает ровно два элемента.

Примечания

Литература

• Weisstein, Eric W. Edge Cover (англ.) на сайте Wolfram MathWorld.
• Michael R. Garey, David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. — W.H. Freeman, 1979. — ISBN 0-7167-1045-5.
• Eugene L. Lawler. Combinatorial optimization: networks and matroids. — Dover Publications, 2001. — ISBN 978-0-486-41453-9.
• М. Свами, К. Тхуласираман. 9.2 Рёберные покрытия // Графы, сети и алгоритмы. — М.: «Мир», 1984. — С. 179-180.

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.