WikiSort.ru - Не сортированное

В теории категорий моноидальные функторы — это функторы между моноидальными категориями, сохраняюющие моноидальную структуру, то есть умножение и тождественный элемент.

Определение

Пусть ${\displaystyle ({\mathcal {C}},\otimes ,I_{\mathcal {C}})}$ и ${\displaystyle ({\mathcal {D}},\bullet ,I_{\mathcal {D}})}$  — моноидальные категории. Моноидальный функтор из ${\displaystyle {\mathcal {C}}}$ в ${\displaystyle {\mathcal {D}}}$ состоит из функтора ${\displaystyle F:{\mathcal {C}}\to {\mathcal {D}}}$ , естественного преобразования

${\displaystyle \phi _{A,B}:FA\bullet FB\to F(A\otimes B)}$

и морфизма

${\displaystyle \phi :I_{\mathcal {D}}\to FI_{\mathcal {C}}}$ ,

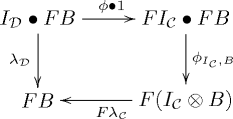
называемых структурными морфизмами, таких что для любых ${\displaystyle A}$ , ${\displaystyle B}$ , ${\displaystyle C}$ в ${\displaystyle {\mathcal {C}}}$ диаграммы

   и   

коммутативны в категории ${\displaystyle {\mathcal {D}}}$ . Здесь используются стандартные обозначения ${\displaystyle \alpha ,\rho ,\lambda }$ для моноидальной структуры категорий ${\displaystyle {\mathcal {C}}}$ и ${\displaystyle {\mathcal {D}}}$ .

Сильно моноидальный функтор — это моноидальный функтор, такой что структурные морфизмы ${\displaystyle \phi _{A,B},\phi }$ обратимы.

Строго моноидальный функтор — это моноидальный функтор, структурные морфизмы которого тождественны.

Пример

Забывающий функтор ${\displaystyle U:(\mathbf {Ab} ,\otimes _{\mathbf {Z} },\mathbf {Z} )\rightarrow (\mathbf {Set} ,\times ,\{*\})}$ из категории абелевых групп в категорию множеств. Здесь структурный морфизм ${\displaystyle \phi _{A,B}\colon U(A)\times U(B)\to U(A\otimes B)}$  — это сюрьекция, индуцированная стандартным отображением ${\displaystyle A\times B\to A\otimes B\to }$ ; отображение ${\displaystyle \phi \colon \{*\}\to \mathbb {Z} }$ переводит синглетон * в 1.

Примечания

• Kelly, G. Max (1974), «Doctrinal adjunction», Lecture Notes in Mathematics, 420, 257—280