WikiSort.ru - Не сортированное

Граф «Лестница»
Вершин	2n
Рёбер	n+2(n-1)
Хроматическое число	2
Хроматический индекс	3 для n>2 2 для n=2 1 для n=1
Свойства	граф единичных расстояний гамильтонов планарный двудольный
Обозначение	Ln

В теории графов лестница L_n — планарный неориентированный граф с 2n вершинами и n+2(n-1) рёбрами ^[1].

Лестницу можно получить как прямое произведение двух путей, один из которых имеет только одно ребро — L_n,1 = P_n × P₁ ^[2][3]. Если добавить ещё два пересекающихся ребра, соединяющих четыре вершины лестницы со степенью два, получим кубический граф — лестницу Мёбиуса.

По построению, лестница L_n изоморфна решётке G_2,n и выглядит как лестница с n перекладинами. Граф является гамильтоновым с обхватом 4 (если n>1) и хроматическим индексом 3 (если n>2).

Хроматическое число лестницы равно 2, а её хроматический многочлен равен ${\displaystyle (x-1)x(x^{2}-3x+3)^{(n-1)}}$ .

Кольцевой лестничный граф

Кольцевой лестничный граф CL_n — это прямое произведение цикла длины n≥3 и ребра ^[4]. В символьном виде CL_n = C_n × P₁. Граф имеет 2n вершин и 3n рёбер. Подобно лестницам граф является связным, планарным и гамильтоновым, но граф является двудольным тогда и только и тогда, когда n чётно.

Галерея

• 
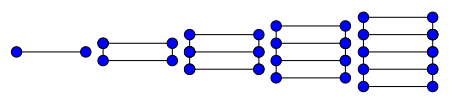
  Хроматическое число лестницы равно 2.

Примечания

Литература

• H. Hosoya, F. Harary. On the Matching Properties of Three Fence Graphs // J. Math. Chem.. — 1993. — Вып. 12. — С. 211-218.
• M. Noy, A. Ribó. Recursively Constructible Families of Graphs // Adv. Appl. Math. — 2004. — Вып. 32. — С. 350-363.
• Yichao Chen, Jonathan L. Gross, Toufik Mansour. Total Embedding Distributions of Circular Ladders // Journal of Graph Theory. — 2013. — Т. 74, вып. 1. — С. 32–57. — DOI:10.1002/jgt.21690.

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.