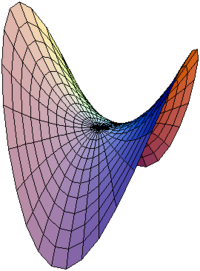
Гиперболическая точка поверхности — в дифференциальной геометрии точка двухмерной поверхности, в которой гауссова кривизна поверхности отрицательна. В гиперболической точке главные кривизны имеют противоположный знак[1].
Связанные определения
Седловая точка поверхности
Седловая точка поверхности — такая точка, что поверхность лежит локально по разные стороны от своей касательной плоскости проведённой в этой точке. Для дважды непрерывно дифференцируемой поверхности из этого следует, что гауссова кривизна в этой точке неположительна. Любая гиперболическая точка является седловой[2].
Некоторые авторы используют термин «седловая точка поверхности» как синоним для «гиперболическая точка поверхности»[1].
Седловая поверхность
Поверхность, у которой каждая точка является гиперболической, называется седловой поверхностью.
Примечания
- 1 2 Роджерс Д., Адамс Дж. Математические основы машинной графики.. — М.: Мир, 2001. — С. 419. — 604 с.
- ↑ Седловая точка — статья из Математической энциклопедии. Д. Д. Соколов.
| Это заготовка статьи по математике. Вы можете помочь проекту, дополнив её. |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .