WikiSort.ru - Не сортированное

Орграф называется сильно связным (англ. strongly connected), если любые две его вершины сильно связны. Две вершины s и t любого графа сильно связны, если существует ориентированный путь из s в t и ориентированный путь из t в s. Компонентами сильной связности орграфа называются его максимальные по включению сильно связные подграфы. Областью сильной связности называется множество вершин компоненты сильной связности.

Определения

Орграф, не принадлежащий к классу сильно связных графов, содержит некоторый набор сильно связных компонент, и некоторый набор ориентированных ребер, идущих от одной компоненты к другой.

Любая вершина орграфа сильно связна сама с собой.

Алгоритмы

Простейший алгоритм решения задачи о поиске сильно связных компонент в орграфе работает следующим образом:

1. При помощи транзитивного замыкания проверяем, достижима ли t из s, и s из t, для всех пар s и t.
2. Затем определяем такой неориентированный граф, в котором для каждой такой пары содержится ребро.
3. Поиск компонент связности такого неориентированного графа даст нам компоненты сильной связности нашего орграфа.

Очевидно основное время работы данного алгоритма приходится на реализацию транзитивного замыкания.

Также существует три алгоритма, решающих данную задачу за линейное время, то есть в V раз быстрее, чем приведенный выше алгоритм. Это алгоритмы Косарайю, Габова и Тарьяна.

Пример

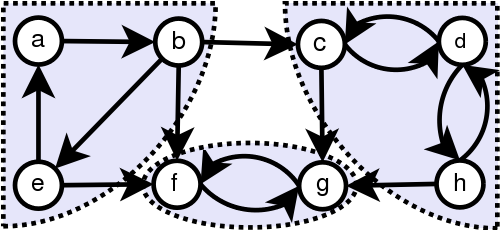
На данном примере изображен орграф, для которого найдены все три компоненты сильной связности (закрашенные области, обведенные пунктиром).

Литература

• Роберт Седжвик. Алгоритмы на графах = Graph algorithms. — 3-е изд. — Россия, Санкт-Петербург: «ДиаСофтЮП», 2002. — С. 496. — ISBN 5-93772-054-7.

Это заготовка статьи по математике. Вы можете помочь проекту, дополнив её.