WikiSort.ru - Не сортированное

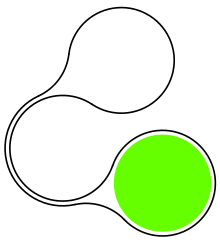
Теорема Пестова — Ионина — классическая теорема дифференциальной геометрии плоских кривых, обобщение теоремы о четырёх вершинах.

Теорема сформулирована Абрамом Ильичом Фетом, доказана Германом Гавриловичем Пестовым, его доказательтво существенно упрощено Владимиром Кузьмичём Иониным^[1]. Для выпуклых кривых результат был известен существенно раньше.^[2]

Формулировка

Любая область плоскости, ограниченная гладкой замкнутой кривой с кривизной не более 1, содержит круг радиуса 1.

Вариации и обобщения

• Из доказательства Пестова и Ионина следует более сильное утверждение: для любой простой гладкой замкнутой регулярной кривой на плоскости существуют две точки соприкасающаяся окружность в которых содержится в замкнутой области внутри кривой; также существуют две точки соприкасающаяся окружность в которых содержится во внешней замкнутой области кривой.
  • Точки в которых соприкасающаяся окружность лежит по одну сторону от кривой являются вершинами кривой, а значит приведённое утверждение является усилением теоремы о четырёх вершинах.

• Аналогичный результат в пространстве не верен, а именно существуют вложения сферы с главными кривизнами, не превосходящими 1 по абсолютной величине, такие, что ограниченная ею область не содержит шара радиуса 1. ^[3]

Примечания